검색결과 리스트
글
※이 내용을 이해하기 위해서는 아래의 내용이
선행되어야 합니다
(이상기체 상태 방정식 유도)
https://sseong40.tistory.com/11
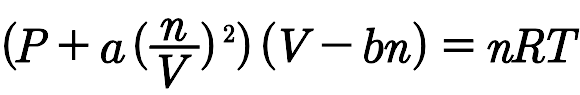
반데르발스 상태 방정식은,
이상기체 상태방정식의 상위 호환입니다!
이상기체에는 5가지 가정이 있어욧
이 5가지 중 2가지 제약을 없앤 방정식이 바로
반데르발스 상태 방정식이며,
남은 3가지 제약을 가지는 기체를
반데르발스 기체라고 합니다~
좀 더 현실에 가깝게 거동하는 기체지요!
-반데르발스 상태방정식 유도

위에서 보신 대로 반데르발스 상태방정식은
이런 형태를 띄고 있습니다!
이상기체 상태방정식과 느낌이 유사하죠?
한 번 어떻게 변했는지 비교해봅시다!

아하! 압력은 좀 더 들어가고,
부피는 조금 더 줄었네요~
여기서 쫌 직관적인 느낌을 받아볼까요?
일단 첫번째로,
부피가 약간 줄어들게 되는 이유는
실제 기체는 입자가 차지하는 부피가 쪼금
있을테니, 고만큼의 부피를 빼주면
약간 줄어들게 되는 겁니다!
두번째로,
압력이 약간 증가하는 이유는
우리는 이상기체 상태 방정식에서는 입자의
인력 같은건 개나 줘버렸지요?
그러니까, 실제 기체는 자신의 순수 압력에서
그들간의 인력이 압력을 상쇄하므로,
측정되는 값은 원래 압력보다 조금 작습니다!
따라서 우리는 인력이 상쇄하는 만큼,
압력의 크기를 조금 더해줄 필요가 있는거죠~
이제 저 위의 식에서 압력이 증가되는 이유와
부피가 감소하는 이유를 이해하셨지요?

그러면 바로 넘어갈게요~
이 녀석은 이상기체 상태방정식의 변형이에요!
V_n이라는 녀석은 V/n입니다~
즉, 부피를 몰수로 나눴으니
단위 몰당 부피, 이를 몰 부피라고 하겠습니닷

다시 또 넘어가서,
이번에는 앞서 말씀드린
입자들 사이의 인력 F에 대해 생각해보죠!
이 인력 F는 1몰 부피당 질량 ,즉 밀도
(오른쪽 녀석인 로우_n)
에 비례해야 맞겠지요?
즉, 1몰 부피라는 기준치인 덩어리가 비좁게
모여있을수록 밀도는 작아지고,
그러면 가까울수록 반발력이 생기니까
인력은 당연히 줄어들겠지요!
(가까워질수록 인력의 증가폭보다,
반발력의 증가폭이 더 큽니다~)
따라서 밀도, 즉 1몰 부피당 질량과 인력은 비례!
그런데 질량은 입자 수인 몰수와 비례하므로,
1몰 부피당 질량과 몰수와 인력은 비례!
따라서 1몰 부피당 질량 뿐만 아니라,
1몰 부피당 몰수와 인력도 비례하겠지요?

당연히 부피가 클수록 인력은 떨어지니,
인력과 부피는 반비례!

여기서 정리를 좀 해주면 다음과 같네요~

이제 이 녀석을 적절한 비례상수를 붙여줘서
두 값이 같다고 해줘도 문제가 없겠군요!

넵 비례상수 a를 넣어줬습니다~

그럼 분모에 있는 압력에,
앞서 구한 인력을 더해주면 되겠네요!

여기서,
기체의 부피에는 순수 기체 부피만이 아닌
기체 입자 자체의 크기도 포함되어 있으니까,
입자의 수(몰수) n에 크기의 비례상수 b를
곱해서 더해주시면 되겠습니다!

그 다음 이 친구를 쫌 정리해주시면 완성!
원래는 엄밀한 증명이 있습니다만..
너무 어려운지라..ㅠㅜ
다음에 기회가 되면 쉽게 풀어서 올릴게욧
빠이~😆
'과학' 카테고리의 다른 글
| [물리1] 시간 지연 공식의 증명 (특수 상대성 이론) (0) | 2019.04.07 |
|---|---|
| [일반물리] 회전 관성 (관성 모멘트) 유도 (0) | 2019.04.07 |
| [유체역학] 베르누이 방정식 유도 (1) | 2019.04.07 |
| [고등화학]이상기체 상태 방정식 유도 (1) | 2019.04.07 |


RECENT COMMENT