검색결과 리스트
글
위의 표기는 x에 대한 f의 편도함수를 뜻해요!
차차 내용을 알아가보겠습니다~
-편미분의 정의
우선 편미분은 다변수 함수에 대한 미분이에요!
(1) : 독립변수가 하나인 일변수함수
(2) : 독립변수가 두개인 다변수함수
(이 경우는 이변수함수)
우리가 (1) 같은 x에 대한 미분은 배우셨을 거에요!
하지만 이제는 x 한 개 뿐만이 아니라,
2개 이상의 변수를 가진 함수를 미분하려 해요~
그런데 2개 이상의 변수부터는 머리가 좀 아프죠?
그렇기 때문에 변수 하나 빼고는 모두 고정하고,
즉 나머지를 모두 상수로 취급해준 상태로
미분을 취하는 것이 바로 편미분이지요!
예를 들면, x y z가 있는 다변수함수에서 x에 대한 편미분은,
y와 z를 상수로 취급해주는 상태에서 미분을 계산합니다~
예를 들어볼까요?
아까 들어본 예시 (2)를 봅시다!
이 녀석을 우선 x에 대하여 편미분 해볼까요?
우리가 하던대로 미분하시면 위와 같게 나와요~
반면 y에 대한 미분은, y 이외의 빨간 친구들이 상수 취급!
따라서 위와 같이 나오게 됩니다~
이제 어렵지 않죠?
이 다음으로는 편미분의 표기를 보겠습니다~
우리가 알던 미분의 표기는 이렇지요?
편미분의 표기는 요런 식입니다!
저 꼬부랭이는 '라운드' 라고 읽어주시면 되어요~
요렇게 쓸 때도 있는데 같은 표기!
뭐..만약 y에 대한 편미분이었다면
그냥 요런 식으로 표시하면 되겠지요?
이 다음으로 편미분의 도함수,
즉 편도함수의 정의도 알아보겠습니다~
우선 요거는 우리가 아는 도함수의 정의죠?
편도함수는 이런 식으로 비스무리하게 정의해요~
(저거는 x에 대한 편미분이니까
x에만 변화 h를 정의해주면 되겠죠!)
만약 y에 대한 편미분이면 요렇게~
(이번에는 y의 변화를 보는 거니까
변화를 뜻하는 h를 y에 넣어주면서 정의!)
여기서 얻어가셔야 할 느낌이 뭐냐하면,
'x에 대한 편미분은 x의 변화만 고려한 미분이다'
이런 느낌을 받아주셔야 해요!
어떤 편미분이 되더라도,
그 변수의 변화에 대해서만 고려한 것이 바로
편도의 미분, 편미분이 되는 겁니다~
질문과 오류 지적은 언제나 환영해요👍
'수학' 카테고리의 다른 글
| [고등미적분] 몫의 미분법 유도 (0) | 2019.04.08 |
|---|---|
| [고등미적분] 곱의 미분법 유도 (0) | 2019.04.08 |
| [고등미적분] 합성함수의 미분법 유도 (연쇄 법칙) (0) | 2019.04.08 |
| [고등미적분] tan , cot , sec , csc 의 미분 유도 (0) | 2019.04.08 |
글

위의 몫의 미분법을 한 번 유도해봅시다!
-몫의 미분법 유도
우선 두 번째 식을 유도해보죠

미분의 정의를 그대로 이용해봅시다~

그렇다면 대입해서 위와 같겠지요?

분자를 통분해줍니다~

여기서 이런 식으로 분리해줘도,
위의 값과 동일하겠죠?

분리한 식을 이렇게 떼주었습니다!
이 두 가지 극한을 계산하면 되네요~

첫 번째 항에서는,
g(x+h)에서 h가 0으로 가면 g(x)가 되겠지요!
두 번째 항에는,
g(x)의 미분의 정의 그대로니까 g'(x)가 됩니다~

따라서 정리해주시면 이렇게 유도되네요!
어렵지 않죠?
이 다음으로 첫 번째 공식을 유도합시다!

요 녀석이었죠?

저 친구를 저렇게 변형해줄 수 있습니다!
여기서 곱의 미분법을 사용해주시면,
(곱의 미분법을 모르신다면 아래로)
https://sseong40.tistory.com/22

다음과 같아지겠네요!

두 번째 항의 1/g(x)의 미분은
위에서 유도해드렸죠?
그걸 대입해봅시다~

첫째 항에 g(x)를 곱하여 통분해줬네요!
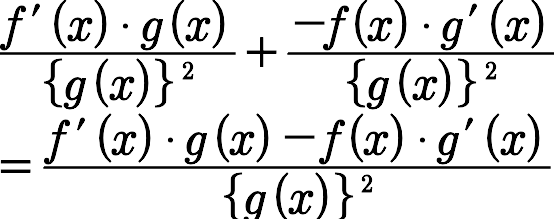
다음 이렇게 합쳐주시면 간단히 유도가 됩니닷
'수학' 카테고리의 다른 글
| [대학미적분] 편미분의 정의 (0) | 2019.04.09 |
|---|---|
| [고등미적분] 곱의 미분법 유도 (0) | 2019.04.08 |
| [고등미적분] 합성함수의 미분법 유도 (연쇄 법칙) (0) | 2019.04.08 |
| [고등미적분] tan , cot , sec , csc 의 미분 유도 (0) | 2019.04.08 |
글

이 녀석이 곱의 미분법이라는 겁니다!
한 번 증명해보죠~
-곱의 미분법 유도

우선 미분의 정의에 따라서,
다음과 같게 나타나겠죠?

이제 여기서 저런 식으로
빨간 녀석을 더하고 뺍시다!
더하고 빼주었으니 당연히 값은 같겠죠~

앞쪽을 g(x+h),뒤쪽을 f(x)로 묶어주었어요!

이런 식으로 극한을 떼보았습니다!
이제 저 두 가지를 계산하면 되겠네요~

첫 항의 첫 번째는 f(x)의 미분의 정의니까 f'(x),
두 번째는 g(x+h)에서 h가 0으로 가니까 g(x)!
두번째 항에서 f(x)는 h와 관련없으니 당연히 h에 대해 극한을 보내봤자 f(x)그대로,
뒤쪽 덩어리는 g(x)의 미분의 정의니까 g'(x)죠?

따라서 위에서 보신 그대로 유도가 되네요!
질문과 오류 지적은 감사히 받겠습니다✅
'수학' 카테고리의 다른 글
| [대학미적분] 편미분의 정의 (0) | 2019.04.09 |
|---|---|
| [고등미적분] 몫의 미분법 유도 (0) | 2019.04.08 |
| [고등미적분] 합성함수의 미분법 유도 (연쇄 법칙) (0) | 2019.04.08 |
| [고등미적분] tan , cot , sec , csc 의 미분 유도 (0) | 2019.04.08 |
글

요 녀석이 합성함수의 미분법입니다!
한 번 유도해볼까요?
참고로 아래와 같이 표현해줄 수도 있어요~

연쇄 법칙(대학 미적분에서 이리 나오는 데, 같은 말)
-합성함수의 미분법 유도

우선 미분의 정의에 따라,
당연히 이렇게 써줄 수 있겠지요?

여기서 위 아래에 같은 값인,
g(x+h)-g(x)를 곱하여 분리해주었네요!
이렇게 해도 당연히 같은 값이겠지요?
저기서 분리된 두 가지 극한을 각각 살펴보면

첫 번째 항은 위와 같은 형태의 미분의 정의이고,

두 번째 항은 위와 같은 미분의 정의입니다!

따라서 첫 항은 f(g(x))의 미분의 정의가 되고
두 번째 항은 g(x)의 미분의 정의가 되므로,
대입해주시면 위와 같은 결과가 유도됩니다~
오류 지적과 질문 항상 환영해요!👍
'수학' 카테고리의 다른 글
| [고등미적분] 몫의 미분법 유도 (0) | 2019.04.08 |
|---|---|
| [고등미적분] 곱의 미분법 유도 (0) | 2019.04.08 |
| [고등미적분] tan , cot , sec , csc 의 미분 유도 (0) | 2019.04.08 |
| [고등미적분] tan x/x , cos x/x 의 극한 유도 (0) | 2019.04.08 |
글
※이 글을 이해하기 위해서는 아래의 내용이
선행되어야 합니다
(각각 sin cos의 미분 , 몫의 미분)
https://sseong40.tistory.com/19
https://sseong40.tistory.com/21

이번에는 앞선 내용들을 이용해서
위의 삼각함수들을 모두 유도해보겠습니다!
-tan x의 미분 유도

우선 탄젠트는 다음과 같지요?
이 녀석에 몫의 미분법을 사용해주시면,

위와 같은 결과가 나오겠지요?
우리는 앞서 sin,cos의 미분을 계산했으므로
이를 대입하면,

다음과 같은 결과가 나옵니다!
이 식을 조금 정리해볼까요?

그러면 위와 같이 나오겠네요!
그런데 저기서
cos제곱+sin제곱=1이 된다는 것 다들 아시지요?
따라서 분자 대신 1을 대입해주시면,

위와 같이 나오게 됩니다!
여기서 조금 더 정리를 해주시면,

요렇게 결과를 유도해줄 수 있어요~
-cot x의 미분 유도

먼저, 코탄젠트는 다음과 같이 정의되지요?
여기서도 몫의 미분법을 사용해주시면,

위와 같은 식이 나오게 됩니다!
여기서도 역시 cos,sin의 미분을 대입하면,

다음과 같이 나오게 되네요~
이 친구를 조금 정리해주면,

위와 같이 나오게 됩니다!
그런데 앞서 말씀드렸듯이
cos제곱+sin제곱=1이 되지요?
따라서 이번에도 1을 대입해주시면,

이렇게 깔끔히 유도되네요~
-sec x의 미분 유도

우선 시컨트의 정의는 위와 같습니다!
이번에도 역시 몫의 미분법~

그렇다면 위와 같게 나오네요!
여기서 cos의 미분을 대입해주시면,

위와 같이 정리되겠지요?
이 녀석을 더 간단히 나타내주자면,

위와 같이 유도해줄 수 있습니다!
-csc x의 미분 유도

마지막으로 코시컨트는 위와 같지요?
몫의 미분을 사용해줍시다!

그렇다면 위와 같이 계산되네요~
조금 더 정리해주면,

위와 같이 간단히 유도됩니다!
질문&오류 지적 항상 환영해요❣
'수학' 카테고리의 다른 글
| [고등미적분] 곱의 미분법 유도 (0) | 2019.04.08 |
|---|---|
| [고등미적분] 합성함수의 미분법 유도 (연쇄 법칙) (0) | 2019.04.08 |
| [고등미적분] tan x/x , cos x/x 의 극한 유도 (0) | 2019.04.08 |
| [대학미적분]역삼각함수의 정의(arcsin , arccos ,arctan) (0) | 2019.04.08 |
글


이번에는 위의 극한을 한 번 유도해봅시다!
-tan x/x의 극한 유도

https://sseong40.tistory.com/20
우선 위의 내용을 보고 오셔야 합니다!

저 글에서 이 부분 기억나시지요?
sin x/x를 유도할 때에는 sin x을 나누었는데,
이번에는 tan x를 나누어보도록 할까요?

그러기 이전에, 이번에도 세타를 다음과 같이
잡아줘볼까요?
(양수쪽으로 잡았으니, 우극한을 보게 되네요)

따라서 위와 같이 나눠줄 수 있습니다!

역수를 취해주면 위와 같이 나오겠지요?

이 식에서 우극한을 한 번 보내봅시다!
(처음에 세타를 양수로 잡았으므로,
좌극한은 음수 쪽에서 와야하니까 우극한만 성립)

그런데 왼쪽 친구는 세타와 관련이 없으니
그대로 1이 나오고,
오른쪽은 그냥 세타에 0을 대입하면
1이 나오네요!
그 값들을 대입했습니다~

따라서 샌드위치 정리에 의해 위와 같네요!

그런데 tan x/x가 우함수인지 볼까요?
만약 우함수라면
0에서의 좌극한과 우극한이 대칭이므로,
좌극한도 1이 되어 결과가 유도되는 겁니다~
(위의 식은 우함수의 성질인 거 아시지요?
저 식이 성립하면 우함수입니다)

그렇다면, x와 -x를 대입해준 이 두 식이 같다면
우함수가 되는 것이겠지요?

그런데 tan x는 기함수이므로
기함수의 성질에 따라
f(-x) = -f(x)가 성립하게 되기 때문에,
결국 tan(-x) = -tan(x)가 되어 식이 성립하네요!

그렇다면 대칭인 좌극한도 위와 같겠지요?

따라서 우극한과 좌극한이 모두 1이므로,
위와 같은 결과를 유도해낼 수 있겠네요~
-cos x/x의 극한은?
혹시나 이 친구의 0으로 갈 때의 극한도
1이라고 충분히 착각할 수 있는데요!
결론부터 말씀드리자면 이 녀석은 발산합니다~

그냥 x에 0을 대입해주시면,

요렇게 해서 발산입니다~
절대 착각하지 마시길!
오류 지적과 질문 대환영👌
'수학' 카테고리의 다른 글
| [고등미적분] 합성함수의 미분법 유도 (연쇄 법칙) (0) | 2019.04.08 |
|---|---|
| [고등미적분] tan , cot , sec , csc 의 미분 유도 (0) | 2019.04.08 |
| [대학미적분]역삼각함수의 정의(arcsin , arccos ,arctan) (0) | 2019.04.08 |
| [고등미적분] sin x/x 극한 유도 (0) | 2019.04.08 |
글
세 녀석들은 각각
sin , cos , tan 의 역함수들인데요!
오늘은 위와 같은 역삼각함수들의 정의에
대하여 알아보도록 하겠습니다~
-arcsin의 정의
먼저, sin의 역함수 arcsin에 대하여 알아봅시다!
우선 sin 함수를 볼까요?

위와 같은 함수인 것 다들 기억나시지요?
그런데 역함수가 존재하기 위해서는
원래 함수가 일대일 함수여야 하기 때문에,
저 sin 함수의 역함수를 정의해주기 위해서는
sin함수가 일대일 함수가 되도록
x의 범위를 잘 잘라줄 필요가 있어요~

그렇다면 위와 같이 정의역으로 잡아주게 된다면,
일대일 함수의 조건을 만족하시는 거 보이시죠?

그러니까 sin함수에서 요렇게만 잘라서 본다는 거죠!
이제 이해되실겁니다~
따라서 저렇게 잘라준다면
이 함수의 정의역과 치역은 각각 아래와 같겠죠?

그렇다면 이 녀석들을 이제 역함수로 바꿔준다면
x와 y가 뒤집히게 되는 것이기 때문에,

역함수인 arcsin의 정의역과 치역은
당연히 위와 같이 나오게 되는 것이지요~
그리고 역함수의 그래프는 y=x에 대하여
대칭인 그래프로 나타나는 것 다들 아실 겁니다!
(x와 y가 뒤바뀌게 되니까 당연히 그렇겠지요?)
그러므로 sin에서 잡아준 정의역만큼을 그대로
대칭이동 시켜준다면,

이런 식으로 빨강->파랑으로 대칭이동 됩니다!
저 파란색이 arcsin 함수가 되는 것이지요~
정리해드리자면,


-arccos 의 정의
다음으로 cos의 역함수에 대하여 알아볼까요?

우선 이 녀석은 cos 함수입니다!
이 녀석도 역함수를 정의해주기 위해서
정의역을 좀 잘라볼까요?

잘라준 정의역과, 그에 따른 치역입니다!
이제 역함수를 만들어주면 이번에도 뒤바뀌죠?

그렇다면 위와 같겠네요~
그럼 이번에도 잘라준 cos의 정의역에 따른
그 역함수 arccos 함수를 그려보자면,

저기서 파란색 cos함수의 0~파이 범위가 딱
뒤집혀서 역함수인 빨간 arccos 함수가 되네요!
어렵지 않죠? 정리하자면,


-arctan의 정의
마지막으로 tan의 역함수입니다!
이번에도 tan 함수를 먼저 보자면,

위와 같이 나오게 되지요~
이번에도 역함수를 만들 수 있게 하기 위해서,
정의역의 범위를 걸어줍시다!

넵 요렇게 나오겠네요~
(이번에는 치역이 실수 전체니까,
딱히 따로 써 줄 필요는 없겠네요!)
그렇다면 당연히 이 녀석의 역함수는,

요런 조건을 가지게 되겠지요?
따라서 잘라준 정의역에 따른 tan의 역함수는
그래프가 아래와 같이 그려집니다~

tan 함수에 있는,우리가 잡아줬던 정의역인
제일 가운데의 빨간 덩어리 하나가 뒤집혀서,
파란색 arctan 함수가 되는 것 보이시죠?
정리하자면,


질문과 오류 지적은 언제나 환영입니닷~✅
'수학' 카테고리의 다른 글
| [고등미적분] tan , cot , sec , csc 의 미분 유도 (0) | 2019.04.08 |
|---|---|
| [고등미적분] tan x/x , cos x/x 의 극한 유도 (0) | 2019.04.08 |
| [고등미적분] sin x/x 극한 유도 (0) | 2019.04.08 |
| [고등미적분] sin , cos 의 미분 유도 (삼각함수) (0) | 2019.04.07 |
글


이번에는 이 녀석을 유도해보도록 하겠습니다!
-sin x/x의 극한 유도
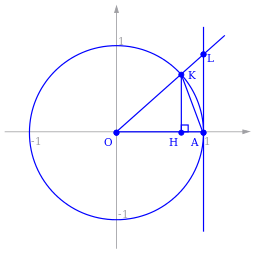
위의 그림을 이용해보도록 하겠습니다!
선분 OA의 길이가 1이고,
각 KOH를 세타라고 합시다!
그렇다면,

각각 요렇게 되는 거 이해되시지요?
여기서,
삼각형 KOH,부채꼴 KOA,삼각형 LOA
이 세 녀석의 넓이 관계에 대해 생각해보죠~
그림을 보시면
삼각형 KOH < 부채꼴 KOA < 삼각형 LOA
요렇게 되는 거 바로 보이실 겁니다!
그러면 저걸 한 번 식으로 써볼까요?

그럼 위와 같이 나오는 거 이해되실 겁니다!
삼각형 넓이 공식,부채꼴 넓이 공식 썼어요~

정리 쫌 해주면 요렇게!

모두 2씩 곱했네요~

여기서 탄젠트는 저렇게 분리되는 거
다들 아시지요?
여기서 sin을 나눌텐데,
그러려면 sin이 0이 아니어야 해요

우선 세타가 위와 같을 때를 살펴볼까요?
(저렇게 뒤쪽에 파이/2를 걸어줘도 되는 이유는,
어차피 우리는 0 근방만 보면 되는 거라서
굳이 양수 전체를 볼 필요는 없으니까 그래요)

그렇다면 요렇게~

역수를 취해주었습니다!

여기서 모두 우극한을 취해볼까요?
좌극한이 안되는 이유는,
이미 각 세타를 양수로 잡아서 그렇습니다!
그런데 저기서 양쪽 녀석들은,
세타에 0을 대입하면 모두 1이 나오는 거
보이시죠?

따라서 위와 같이 나오는데,
샌드위치 정리에 의해 우극한이 1임을
금방 알아낼 수 있습니다

여기서 sin x/x가 우함수인지를 볼까요?
이를 보는 이유는,
우함수라면 0에서의 좌극한과 우극한이
대칭을 이루기 때문에 같겠죠?
따라서 저 함수가 우함수라면,
좌극한도 우극한과 같은 1임을 알 수 있고,
그러므로 0에서의 극한이 1임을 알 수 있겠지요!

자 이렇게 대입해보았습니다!
우변에서 sin(-x)는 -sin x니까
양변이 같으므로 우함수가 맞네요!
(sin x는 기함수니까,
sin(-x)=-sin (x) 인거 다들 아시지요?
기함수의 성질~)

따라서 결국 좌극한이 우극한과 대칭이므로,
좌극한이 우극한과 같은 1임을 알아냈습니다!

따라서 위와 같이 유도되네요!
질문&오류 지적 환영해요👌
'수학' 카테고리의 다른 글
| [고등미적분] tan x/x , cos x/x 의 극한 유도 (0) | 2019.04.08 |
|---|---|
| [대학미적분]역삼각함수의 정의(arcsin , arccos ,arctan) (0) | 2019.04.08 |
| [고등미적분] sin , cos 의 미분 유도 (삼각함수) (0) | 2019.04.07 |
| [고등미적분] 역함수의 미분법 유도 (0) | 2019.04.07 |













RECENT COMMENT