[고등미적분] sin x/x 극한 유도

​

sin x/x 의 그래프

 

 

이번에는 이 녀석을 유도해보도록 하겠습니다!

​

​

​

​

​

​

-sin x/x의 극한 유도

출처 : https://socratic.org/questions/how-do-you-use-the-squeeze-theorem-to-find-lim-sin-x-x-as-x-approaches-zero

 

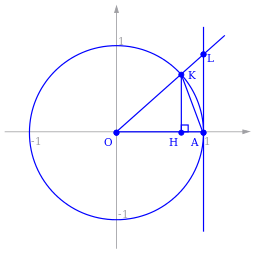
위의 그림을 이용해보도록 하겠습니다!

​

​

​

선분 OA의 길이가 1이고,

각 KOH를 세타라고 합시다!

​

​

그렇다면,

각각 요렇게 되는 거 이해되시지요?

​

​

​

​

여기서,

삼각형 KOH,부채꼴 KOA,삼각형 LOA

​

이 세 녀석의 넓이 관계에 대해 생각해보죠~

​

​

​

​

그림을 보시면

삼각형 KOH < 부채꼴 KOA < 삼각형 LOA

​

요렇게 되는 거 바로 보이실 겁니다!

​

​

그러면 저걸 한 번 식으로 써볼까요?

​

​

​

​

​

그럼 위와 같이 나오는 거 이해되실 겁니다!

​

삼각형 넓이 공식,부채꼴 넓이 공식 썼어요~

​

​

​

​

​

​

정리 쫌 해주면 요렇게!

​

​

​

​

​

​

모두 2씩 곱했네요~

​

​

​

​

여기서 탄젠트는 저렇게 분리되는 거

다들 아시지요?

​

여기서 sin을 나눌텐데,

그러려면 sin이 0이 아니어야 해요

​

​

​

우선 세타가 위와 같을 때를 살펴볼까요?

​

​

​

(저렇게 뒤쪽에 파이/2를 걸어줘도 되는 이유는,

어차피 우리는 0 근방만 보면 되는 거라서

굳이 양수 전체를 볼 필요는 없으니까 그래요)

​

​

​

​

​

​

그렇다면 요렇게~

​

​

​

​

​

​

역수를 취해주었습니다!

​

​

​

​

​

​

여기서 모두 우극한을 취해볼까요?

​

좌극한이 안되는 이유는,

이미 각 세타를 양수로 잡아서 그렇습니다!

​

​

​

그런데 저기서 양쪽 녀석들은,

​

세타에 0을 대입하면 모두 1이 나오는 거

보이시죠?

​

​

​

​

​

따라서 위와 같이 나오는데,

​

샌드위치 정리에 의해 우극한이 1임을

금방 알아낼 수 있습니다

​

​

​

​

​

​

여기서 sin x/x가 우함수인지를 볼까요?

​

​

​

이를 보는 이유는,

​

우함수라면 0에서의 좌극한과 우극한이

대칭을 이루기 때문에 같겠죠?

​

​

​

따라서 저 함수가 우함수라면,

좌극한도 우극한과 같은 1임을 알 수 있고,

​

그러므로 0에서의 극한이 1임을 알 수 있겠지요!

​

​

​

​

​

​

자 이렇게 대입해보았습니다!

​

우변에서 sin(-x)는 -sin x니까

양변이 같으므로 우함수가 맞네요!

​

​

​

​

(sin x는 기함수니까,

sin(-x)=-sin (x) 인거 다들 아시지요?

기함수의 성질~)

​

​

​

​

​

따라서 결국 좌극한이 우극한과 대칭이므로,

​

좌극한이 우극한과 같은 1임을 알아냈습니다!

​

​

​

​

따라서 위와 같이 유도되네요!

​

​

​

​

​

​

질문&오류 지적 환영해요👌

​