검색결과 리스트
글
(이전 강의)
https://sseong40.tistory.com/6
※항등원, 역원의 개념을 모르시고 이 글을 읽으시면 자신이 바보로 느껴질 수 있습니다.
지금까지 행렬의 덧셈에 대하여
다루어 본 것들 기억나시나요?
이제 몇가지 개념을 좀 더 쌓아봅시닷
-덧셈의 항등원(영행렬)
영행렬이라는 친구는,
행렬의 덧셈에서 항등원인 친구입니다!
어떤 행렬 A에 영행렬 O를 더해도,
그 값은 그대로 행렬 A가 되는 그런 행렬이지요~
그렇다면 영행렬의 모든 성분은
반드시 0이 되어야 하겠네요!

만약 위와 같은 행렬 A가 있다면,
행렬 A의 영행렬은 아래와 같겠지요~
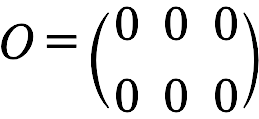
그러니까 정리해드리자면,
영행렬 : 모든 성분이 0인 행렬
이라고 볼 수 있겠습니다~
자 어렵지 않죠?
-덧셈의 역원
그럼 두번째로 덧셈의 역원을 살펴볼까요?
이 역시 아주 간단합니다!
행렬 A가 있다면,
이 행렬 A의 덧셈의 역원은 -1×A= -A 입니다!
한가지 예를 들어볼까요?

행렬 A가 다음과 같다면,역원은 아래와 같습니닷

여기에서 추가적으로 알아야 할 것은,
'행렬의 덧셈은 교환법칙,결합법칙이 성립한다'
는 것인데요!
각각의 성분들을 더해주는 것 뿐이기 때문에,
상수의 연산에 관한 성질을
그대로 띄고 있어서 그렇습니다!
아마 직감하고 계셨을거에요 ㅋㅋ
(다음 강의)
https://sseong40.tistory.com/8
'수학' 카테고리의 다른 글
| [수학1] 자연수 거듭제곱의 합 (시그마 공식) 유도 (0) | 2019.04.07 |
|---|---|
| [기초행렬] 5. 곱셈의 성질과 단위행렬 (0) | 2019.04.07 |
| [기초행렬] 3. 행렬의 의의 (0) | 2019.04.07 |
| [기초행렬] 2. 행렬의 연산 (0) | 2019.04.07 |


RECENT COMMENT