검색결과 리스트
수학에 해당되는 글 21건
- 2019.04.07 [고등미적분] sin , cos 의 미분 유도 (삼각함수)
- 2019.04.07 [고등미적분] 역함수의 미분법 유도
- 2019.04.07 [수학1] 그 외 유용한 시그마 공식 유도 1
- 2019.04.07 [미분적분학] 테일러 급수 유도
- 2019.04.07 [수학1] 수열의 합 공식 유도
- 2019.04.07 [수학1] 자연수 거듭제곱의 합 (시그마 공식) 유도
- 2019.04.07 [기초행렬] 5. 곱셈의 성질과 단위행렬
- 2019.04.07 [기초행렬] 4. 덧셈의 성질과 연산
글

두 삼각함수의 미분이네요!
바로 유도해보도록 합시다
-sin x의 미분

일단 요렇게 써줍시다

그런데 위의 식 기억나시나요?
미분의 정의지요?
따라서 저 녀석의 미분은,

다음과 같이 정의됩니다!
이제 이 녀석을 구하면 되겠네요~

sin (x+h)를 덧셈 정리에 의해,
위와 같이 전개했습니다!

뒤에 있는 sin x를 묶어주었네요~

이런 식으로 극한을 떼어볼까요?
sinx와 cos x는 h와 관련없으니
그냥 저렇게 빠져나가는 것도 가능합니다~

저 위에서 이 녀석을 한 번 계산해보죠!
위아래에 같은 값을 곱합시다

이런 식으로 나오겠네요~

여기서 위쪽이 저렇게 되는 이유 아시겠죠?
cos제곱+sin제곱=1 이라는 기본 공식입니다

저런 식으로 떼볼 수 있겠네요~

첫번째 항은 1이 되고
두번째 항은 sin 0=0이므로 0이 됩니다!
둘을 곱하면 0 이겠죠?
(sin h/h가 왜 1이냐구요?
설명은 아래 링크에 있습니다)
https://sseong40.tistory.com/20

따라서 첫째 항에는 이 0을 대입해주시고,
두 번째 항은 위에 달아둔 링크에서
말씀드렸다시피 1이 나올테니
결국 결과가 도출 가능하네요!
-cos x의 미분

다음으로 cos x의 미분은 요렇겠죠?

역시 cos의 덧셈 정리를 이용!

뒤의 cos x를 묶어주었습니다~

저런 식으로 떼주신 다음,
이번에도 h와 무관한 애들은 밖으로 빠지네요!

위에 나오는 두 가지 극한은
sin x의 유도에서 보여드렸죠?
따라서 이번에도 대입하시면 요렇게 도출되네요!
질문&오류 지적은 언제나 환영입니다❣
'수학' 카테고리의 다른 글
| [대학미적분]역삼각함수의 정의(arcsin , arccos ,arctan) (0) | 2019.04.08 |
|---|---|
| [고등미적분] sin x/x 극한 유도 (0) | 2019.04.08 |
| [고등미적분] 역함수의 미분법 유도 (0) | 2019.04.07 |
| [수학1] 그 외 유용한 시그마 공식 유도 (1) | 2019.04.07 |
글

이번에는 요 녀석을 증명해보도록 하지요~
-역함수 미분법 유도

우선 g(x)을 f의 역함수라고 생각하시면,
다음과 같게 나오겠지요?
정의역 y를 대입하시면 g(x)는
정의에 따라 x가 나올테니,
결국 f(x)=y가 나오니까
결과는 y에 대한 항등함수~
(이거 그냥 역함수의 성질같은 거에욧
혹시 모를까봐 설명드렸슴다)
이 다음에 이 녀석을 미분해볼까요?

이런 식으로 나오겠네요!
합성함수의 미분법을 그대로 사용했습니다~
(합성함수의 미분법을 모르신다면 아래로)

위의 녀석을 조금 변형했습니다!

이제 여기서 앞서 말씀드렸듯이,
g(x)를 f의 역함수라고 말씀드렸죠?
그래서 위와 같이 바꿨습니닷
어렵지 않쥬?
질문,오류 지적 언제나 환영해요👍
'수학' 카테고리의 다른 글
| [고등미적분] sin x/x 극한 유도 (0) | 2019.04.08 |
|---|---|
| [고등미적분] sin , cos 의 미분 유도 (삼각함수) (0) | 2019.04.07 |
| [수학1] 그 외 유용한 시그마 공식 유도 (1) | 2019.04.07 |
| [미분적분학] 테일러 급수 유도 (0) | 2019.04.07 |
글
※이 내용을 보기 위해서는 아래의 내용이
선행되어야 합니다
https://sseong40.tistory.com/9

이번에는 요 녀석들을 유도해볼까 합니다!
1.제곱수의 시그마 공식

우선 요 녀석을 증명합시다~
좌변은 아래와 같이 나타낼 수 있겠지요?

(요거 시그마 연산의 성질입니다!
저렇게 분배해주거나, k랑 관련 없는 녀석들은
밖으로 빼고 하는 게 가능~)

여기서, 우리가 앞서 배운
자연수 총 합의 공식을 대입해줍시다!
또한, 1을 n번 더한 것은 n이라고 말씀드렸죠?
이 녀석 역시 대입~

그럼 요렇게 간단히 표현됩니다!
이 녀석을 쫌 정리해주면 n^2이 나오는 거
금방 아실거에요~

그러면 결국 n^2이 좌변의 결과가 된다는
것이로군요!
이렇게 첫 번째 증명은 끝~
어렵지 않죠?
2. k(k+1) 시그마 공식

이 친구도 한 번 유도해봅시닷

얘도 그냥 시그마의 연산을 해준거 뿐이지요!
그냥 단순하게 분리만 좀 해줬습니다~

이제 여기에서,
우리가 앞서 유도한 자연수 제곱의 총 합 공식과
자연수의 총 합 공식을 대입해주면,
다음과 같겠네요~

여기서 이 친구를 쫌 정리해주면 요렇게
나오게 되네요!
이렇게 해서 두 번째까지 증명 완료~
3.k(k+1)(k+2)시그마 공식

마지막으로 얘를 증명해볼 차례네요!
이번에도 역시, 앞서 증명 방법과
상당히 유사하게 흘러가요~

우선 안의 항들을 모두 전개!

그 다음에는 우리가 앞서 해준 것처럼
항들을 각각 분리해주었네요~

그 다음에는 순서대로,
자연수 세제곱 합,자연수 제곱 합,자연수 합
공식을 대입해줍니닷
그러면 위와 같겠네요!

이 녀석을 쫌 계산해줘서
간단히 표현해보았습니다~
그러면 결과가 위와 같게 나오네요!
이렇게 마지막 공식까지 간단히 증명👍
오류나 궁금하신 부분 언제든지 말씀해주세욧
항상 열려있슴다😆
'수학' 카테고리의 다른 글
| [고등미적분] sin , cos 의 미분 유도 (삼각함수) (0) | 2019.04.07 |
|---|---|
| [고등미적분] 역함수의 미분법 유도 (0) | 2019.04.07 |
| [미분적분학] 테일러 급수 유도 (0) | 2019.04.07 |
| [수학1] 수열의 합 공식 유도 (0) | 2019.04.07 |
글
※이 내용을 이해하기 위해서는 고등 미적분을
보고 오셔야 합니다!

위의 살벌한 녀석은 바로 테일러 급수!
초월함수들을 다항함수로 바꿔서
계산을 용이하게 해주는,
수학에서 광범위하게 쓰이는 중요한 녀석이죠~
바로 유도에 들어가보도록 하겠습니닷
-테일러 급수의 유도

우선은 어떤 복잡한 함수 f(x)를
저런 형태의 다항함수로 분해하려고 합니다!
우선 조건을 좀 걸어줄게요~
-함수 f(x)는 x=a에서 무한 번 미분 가능하다.
참고로 여기서, 일반적인 다항함수인
a+bx+cx^2 ...로 두지 않고 저렇게 둬도
괜찮을까 생각이 들 수도 있는데요!

저 다항식은 결론적으로는 모두 전개하면,
아래와 같은 일반적인 다항함수가 나오는 거
이해되시죠?
저런 형태로 유도한 뒤에 그냥 전개해버리면
되는 문제니까,
그냥 편의상 모양을 저렇게 잡아준거다~
라고 생각하시면 되겠습니다!

그러면 함수 f(x)에 a를 대입해볼까요?
그러면 결과는 위와 같이 나오게 되겠네요~

여기서, 이 함수 f(x)를 미분해봅시다!
그러면 미분된 함수 f'(x)는 위와 같겠죠?

계속해서 또 a를 대입!

이번에는 미분한 함수를 또 미분해서,
2회 미분합니다!

이번에는 대입하니 이렇게 나오네요!

마찬가지로, 3회 미분에 a를 대입해주시면
위와 같은 답이 나오게 됩니다!

지금까지 나온 결과값들을 쭈욱 나열해서
c들에 대하여 정리했습니다!
( ex)f'''(a)=3!×c_2 를 c_2에 대해 정리하면,
c_2=f'''(a)/3! )
이제 규칙이 확연히 보이시죠?

아까 제가 잡아둔 다항함수 식에 c들의 값을
모조리 대입해보았습니다!

대입해준 녀석들을
시그마를 이용해 묶어주었어요!
이렇게 테일러 급수를 유도해냈습니다~
(앞서 말씀드렸지만,
f(x)가 x=a에서 무한 번 미분 가능해야합니다!
그래야 f의 1,2,3...∞차 미분이 존재..)
-맥클로린 급수
테일러 급수에서 a=0인 특별한 경우의 급수를,
맥클로린 급수라고 합니다!
식은 아래와 같겠네요~

맥클로린 급수
a=0을 대입해준 것 뿐!
어렵지 않죠?
(이 녀석도 당연히 x=0 무한 번 미분 가능해야..!)
예제1)다음 함수를 테일러 급수로 변환하라.

답 :
1.

'수학' 카테고리의 다른 글
| [고등미적분] 역함수의 미분법 유도 (0) | 2019.04.07 |
|---|---|
| [수학1] 그 외 유용한 시그마 공식 유도 (1) | 2019.04.07 |
| [수학1] 수열의 합 공식 유도 (0) | 2019.04.07 |
| [수학1] 자연수 거듭제곱의 합 (시그마 공식) 유도 (0) | 2019.04.07 |
글

고등학교에서 배우는 대표적인 수열로는
등차수열과 등비수열이 있겠는데요!
이 두가지 수열들의 총합을 계산하는
공식을 한 번 유도해봅시다~
-1.등차수열의 합 공식 유도
우선 등차수열의 합 공식부터 유도해볼까요?
일단 제 1항부터 제 n항까지의 등차수열 합은
다음과 같이 나타나요!

제 1항부터 제 n항까지의 값을
순서대로 쭈욱 더했습니다~

그런데 여기서 합을 쪼금 달리 표현해볼게요!
a는 첫 항인 제 1항, 값은 a+(1-1)d=a
l은 마지막 항인 제 n항, 값은 a+(n-1)d
저기서 아래쪽 합은 마지막 항인 제 n항에서부터
공차 d씩 순서대로 빼가면서,
더하는 순서를 거꾸로 해주는 것 뿐이에요~

여기서 이 두 녀석을 더해보았습니다!
흥미롭게도 모두 a+l 이라는 값이..!

그런데 이 a+l이 총 n개 있는 것이므로,
(a+l)×n개 , 즉 n(a+l)로 나타내줄 수 있겠죠?

그럼 여기서 2를 나눠주면 총 합 S 유도 끝~

여기서 쪼금 더 가보자면,
마지막 항인 제 n항의 값은
a+(n-1)d라고 제가 말씀 드렸죠?
그 녀석을 대입해주면 저렇게 나와요~
둘 다 암기하고 계셔야 합니닷
-2.등비수열의 합 공식 유도

비슷한 흐름으로,
등비수열의 제 1항부터 제 n항까지의 합은
다음과 같이 나타나요!

여기서, 총 합 S에 r을 곱해주시면
아래와 같은 결과가 나오는 것 쉽게 이해되시죠?

위의 녀석에서 아래를 빼보았습니다~
위와 같이 소거되니까
남는 녀석은 아래와 같게 나오겠네요!
( 좌변은 S-rS니까 S로 묶어주시면
(1-r)S 입니닷 )

여기서 또 S에 대해 식을 바꿔주시면
다음과 같은 결과가 도출됩니다!
그런데 1-r을 나누려면,
r이 1이 아니라는 조건이 있어야겠죠?
그렇다면 r=1일 때는 어떨까요?

r=1이라면 이렇게 아주 간단히 나오네요!
예제1)다음 수열의 제 1항부터 제 15항까지의
총 합은 얼마인가?

예제2)다음 수열의 제 3항부터 6항까지의
총 합은 얼마인가?

답 :
1. 공식을 그대로 이용한다.

2. 제 6항까지의 합 - 제 2항까지의 합.

'수학' 카테고리의 다른 글
| [수학1] 그 외 유용한 시그마 공식 유도 (1) | 2019.04.07 |
|---|---|
| [미분적분학] 테일러 급수 유도 (0) | 2019.04.07 |
| [수학1] 자연수 거듭제곱의 합 (시그마 공식) 유도 (0) | 2019.04.07 |
| [기초행렬] 5. 곱셈의 성질과 단위행렬 (0) | 2019.04.07 |
글

이 세가지 계산에 대한 증명을 해보도록
하겠습니다!
일단 저 세가지가 어떤 것인지부터 알아야죠~
왼쪽부터 순서대로,

요런 녀석들을 계산하게 해주는
식들이랍니다!
우선 결과부터 쭈욱 보여드릴게요~

자 그럼 순서대로 유도해보도록 할게요!
-1. 자연수 n의 총 합

우선 n까지의 자연수의 총 합 S는 위와 같이
나타낼 수 있겠죠?

그런데, 아래처럼 순서를 바꿔도 당연히
값은 S 그대로겠죠~
여기서 이 두 녀석을 더해보면,

이렇게 신기하게도 전부 n+1이 나오네요!
근데 이 녀석들이 n개 있는 게 되는 것이니,

요렇게 간단하게 나타내줄 수 있겠죠?
여기서 양변에 2를 나눠주시면

다음과 같이 나오네요!
그런데 저 S가 앞서 말씀드린대로
자연수 n까지의 총합이 되는 것이니,

요렇게 되는 것이겠네요!
이렇게 해서 첫번째 공식의 증명 완료~
2.자연수 n의 제곱의 총 합
바로 다음 녀석으로 넘어가보도록 하죠!

이번에는 위의 식을 써먹어서
증명을 하려고 합니다!
(저거 이해 안되시진 않겠죠..?
그냥 좌변을 전개해서 우변이 나오는 것!)

일단 1부터 n까지 각각 대입해서,
전체 식의 총 합을 표현해봅시다!

이제 이 녀석들을 더하는 작업을 하면 되는데,
좌변이 저런 식으로 깔끔히 소거되죠?
계속 이어가봅시다~

그러면 당연히 이렇게 나오겠네요!
음..우변이 조금 헷갈릴 수 있는데,
첫번째 항 :

두번째 항 :

세번째 항 :

위와 같은 녀석들입니다~
이렇게 보시면 이해가 금방 되실거에요!

좌변은 그냥 계산하시면 되고,
우변의 세번째 항은 1을 n번 더했기 때문에
1×n 하셔서 n이 나오게 됩니다!
그런데 아까 말씀드렸다시피,

요렇다고 유도해드렸죠?
이 녀석을 저기 대입해주시면,

요렇게 되네요~
이제 저 시그마가 붙은 식에 대하여
정리해보도록 하겠습니다!
(단순 계산이에욧)

자 이렇게 유도를 해냈습니다!
3.자연수 n의 세제곱의 총 합
이제 마지막 공식이네요!

이번엔 위의 녀석을 이용~
아까랑 정말 비슷한 흐름이에요!
여기서 또 1부터 n까지 대입하시면,

요렇겠죠?
이 친구들을 모조리 더해봅시다!

그러면 좌변이 요렇게 소거되면서
간단히 표현됩니다!
이제 모두 더한 식을 표현해주시면,

위와 같겠네요!
우변은 이제 간단히 이해되시죠?
(안되면.. ㅂㄷㅂㄷ)

좌변을 쫌 정리했어요~
이제 여기서 아까 구한 두 녀석들을
그대로 대입해봅시다!

그럼 요렇게 나오겠네요!
이제 얘를 시그마 식에 대해 정리해주면,

이번에도 간단히 유도 끝!
오류 있거나 궁금한 점 있으신 분들
댓글로 언제든지 환영이에요~
그럼 빠이! 😘
'수학' 카테고리의 다른 글
| [미분적분학] 테일러 급수 유도 (0) | 2019.04.07 |
|---|---|
| [수학1] 수열의 합 공식 유도 (0) | 2019.04.07 |
| [기초행렬] 5. 곱셈의 성질과 단위행렬 (0) | 2019.04.07 |
| [기초행렬] 4. 덧셈의 성질과 연산 (0) | 2019.04.07 |
글
(이전 강의)
https://sseong40.tistory.com/7
※항등원, 역원의 개념을 모르시고 이 글을 읽으시면 자신이 바보로 느껴질 수 있습니다.
앞선 글에서 덧셈의 항등원과 역원에 대하여
다루어보았습니다!
이번에는 곱셈에 대해서도 다루어봐야겠죠?
바로 시작해보도록 합시다!
-곱셈의 항등원(단위행렬)
단위행렬이라는 녀석은 아주 간단합니다!
어떤 행렬 A에 이 단위행렬 E를 곱해서 행렬 A가 나오도록 해주는 행렬을 말하지요~
단위행렬은 다음과 같은 녀석들입니다!

각각 1차,2차,3차 단위행렬이라고 불러요~
행이 1개인 녀석은 1차,
2개인 녀석은 2차,3개는 3차에
곱해주시는 방식이면 되겠습니다!
예시를 하나 들어볼까요?
다음과 같은 행렬 A의 단위행렬이 뭘까요?

행이 2개니까 2차 단위행렬에 해당하네요~
그러면 정말 항등원이 맞는지 직접 곱해보죠!

오호, 정말 그렇게 나오네요!
( 1이 살려줄 성분 한 가지만 살리고,
남은 자리의 0들이 나머지 성분들을 없애주는
모습이 보이신가요? )
이렇게 해서 단위행렬에 대해 알아보았으니,
다음으로 곱셈의 역원, 역행렬을 알아보죠!
-곱셈의 역원(역행렬)
곱셈에도 당연히 역원이 존재합니다!
행렬 A의 역행렬은

으로 표기해줍니다~
역원의 정의에 따라 행렬 A에 역행렬을 곱하면,
당연히 항등원인 단위행렬이 나와야겠지요?
그렇다면 이 사실을 이용해서
역행렬을 공식으로 유도해보려고 했지만..!
글이 너무 어렵고 길어질 것 같아서
2×2행렬의 경우만 써드리도록 하겠습니닷..ㅠㅠ
(det, adj 같은 녀석들이 나오는지라..)
-2×2 행렬의 역행렬 공식 유도
우선 행렬 A과 그 역행렬 X를 잡아줍시다~

요렇게 말이지요!
여기서 이 둘을 곱하게 되면,
행렬×역행렬이니까 당연히 단위행렬이 나오겠네요~
그렇게 식을 세워서 계산을 해봅시닷

세워서 계산하니까 요렇게 나오는군요!
그런데 저 녀석이 성립하려면,
각 성분이 같아야 하는거 아니겠어요?

따라서 위와 같은 식이 성립해야 하네요!
이 네가지 식을 이용해서,
역행렬의 성분인 w,x,y,z를 a,b,c,d에 관한
식으로 나타낼 수 있어요!
w를 그렇게 구해볼까요?
그러면 다음과 같은 결과가 나와요!

나머지 x,y,z 도 같은 방법으로 풀 수 있어요!
그래서 이렇게 구한 w,x,y,z를 모두 대입하면,

이렇게 나오게 되네요!
이렇게 해서 2×2 행렬의 역행렬 공식을
유도해내었습니다~
그런데 저기서 분모 ad-bc=0이면,
즉, ad=bc이면 말이 안되는 거잖아요?
따라서 ad=bc인 2×2행렬은 역행렬을
가지지 못합니다 ㅠㅠ
(여기서 ad-bc를 판별식,
ad≠bc라서 역행렬을 가지는 녀석들을
가역행렬 이라고 부릅니닷!)
-역행렬의 성질
앞서 배운 역행렬은 다양한 성질을
가지고 있는데요!
하나씩 알아보도록 하죠~

일단 기본적으로 위의 3가지는
알아두시는 게 좋을 것 같아요!
1 :
이건 그냥 역행렬의 정의죠? ㅋㅋ
2 :
뒤집은 놈을 또 뒤집으면 당연히 원래대로~
3 :
행렬의 곱셈은 교환법칙이
성립하지 않기 때문에 이런 형태에요!
우변에 행렬 AB를 곱해보시면
금방 알 수 있겠네요~

위처럼 곱해보시면 둘 다 성립!
앞서 언급한 것에도 나오듯
아주 중요한 사실은,
교환법칙과 결합법칙이
둘 다 성립하는 행렬의 덧셈과는 달리,
행렬의 곱셈은 결합법칙은 성립하지만
교환법칙이 성립하지 않아요!
(AB≠BA라는 소리,
이는 반례를 찾아 쉽게 증명 가능합니다!)
대신 단위행렬 E와 행렬 A의 곱은
교환법칙이 성립합니다~
(이 역시 계산으로 쉽게 알 수 있겠죠!)
예제1) 다음을 증명하라.

예제2)다음 행렬 A의 역행렬을 구하라.

예제3)다음 행렬의 역행렬이 존재하는가?

답 :
1.양변을 각각 행렬의 곱셈을 취하면
쉽게 증명 가능하다.
2.

3. O , X
'수학' 카테고리의 다른 글
| [수학1] 수열의 합 공식 유도 (0) | 2019.04.07 |
|---|---|
| [수학1] 자연수 거듭제곱의 합 (시그마 공식) 유도 (0) | 2019.04.07 |
| [기초행렬] 4. 덧셈의 성질과 연산 (0) | 2019.04.07 |
| [기초행렬] 3. 행렬의 의의 (0) | 2019.04.07 |
글
(이전 강의)
https://sseong40.tistory.com/6
※항등원, 역원의 개념을 모르시고 이 글을 읽으시면 자신이 바보로 느껴질 수 있습니다.
지금까지 행렬의 덧셈에 대하여
다루어 본 것들 기억나시나요?
이제 몇가지 개념을 좀 더 쌓아봅시닷
-덧셈의 항등원(영행렬)
영행렬이라는 친구는,
행렬의 덧셈에서 항등원인 친구입니다!
어떤 행렬 A에 영행렬 O를 더해도,
그 값은 그대로 행렬 A가 되는 그런 행렬이지요~
그렇다면 영행렬의 모든 성분은
반드시 0이 되어야 하겠네요!

만약 위와 같은 행렬 A가 있다면,
행렬 A의 영행렬은 아래와 같겠지요~
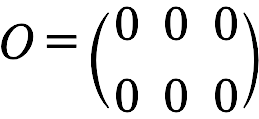
그러니까 정리해드리자면,
영행렬 : 모든 성분이 0인 행렬
이라고 볼 수 있겠습니다~
자 어렵지 않죠?
-덧셈의 역원
그럼 두번째로 덧셈의 역원을 살펴볼까요?
이 역시 아주 간단합니다!
행렬 A가 있다면,
이 행렬 A의 덧셈의 역원은 -1×A= -A 입니다!
한가지 예를 들어볼까요?

행렬 A가 다음과 같다면,역원은 아래와 같습니닷

여기에서 추가적으로 알아야 할 것은,
'행렬의 덧셈은 교환법칙,결합법칙이 성립한다'
는 것인데요!
각각의 성분들을 더해주는 것 뿐이기 때문에,
상수의 연산에 관한 성질을
그대로 띄고 있어서 그렇습니다!
아마 직감하고 계셨을거에요 ㅋㅋ
(다음 강의)
https://sseong40.tistory.com/8
'수학' 카테고리의 다른 글
| [수학1] 자연수 거듭제곱의 합 (시그마 공식) 유도 (0) | 2019.04.07 |
|---|---|
| [기초행렬] 5. 곱셈의 성질과 단위행렬 (0) | 2019.04.07 |
| [기초행렬] 3. 행렬의 의의 (0) | 2019.04.07 |
| [기초행렬] 2. 행렬의 연산 (0) | 2019.04.07 |


RECENT COMMENT